Cavitation and NPSH

What is Cavitation?

Cavitation occurs when the absolute pressure at the eye of the impeller falls below the vapor pressure of the liquid being pumped. When this occurs, vapor bubbles or “cavities” form in the liquid. As the bubbles move from the low-pressure area near the impeller toward the high-pressure area near the pump discharge, they implode violently back to their liquid state.

These little implosions of collapsing bubbles sometimes cause loud popping noises which can be heard externally when the pumps are operating. Internally, this ongoing process of implosion creates shockwaves that can result in considerable physical damage. Over time, cavitation can destroy impellers and pump housings, cause seal and bearing failure, impact flow and pressure, and consume significantly more power.

Image 2: Cavitation Damage on Pump Impeller

Reduce the Chance of Cavitation

As long as NPSH_A > NPSH_R, cavitation will not happen. NPSH_R is a characteristic of the pump and is readily available from its manufacturer for a given duty condition. NPSH_A is a function of the entire “system” feeding the pump, which will include:

• The temperature and vapor pressure of the liquid being pumped
• The absolute pressure on the free surface of the liquid (usually atmospheric pressure but not always)
• The size and length of the suction piping and all pipe fittings (e.g., elbows, tees, etc.)
• The height of the liquid in the supply tank above or below the pump’s centerline

Figure 1: Net Positive Suction Head (NPSH)

The calculation of NPSH_A looks like this:

Equation 1

• H_ps = The absolute pressure on the surface of the liquid in the tank supplying the pump. In an open-top tank, this is simply atmospheric pressure. But in an enclosed (closed top) tank this could be either higher or lower (vacuum) than atmospheric pressure. (Remember that atmospheric pressure by definition is zero-gauge pressure but always a positive number in absolute terms.) NPSH_A is always calculated using absolute terms. It also must be given in terms of head of the liquid being pumped. This will require conversion from units of pressure to units of head.
• H_ss = The static suction head either above or below the pump centerline. This number is usually positive but is negative in cases where the pump is above the liquid level in the supply tank (e.g., a suction lift condition).
• H_f = The piping entrance and friction losses from the supply tank to the pump’s suction flange. H_f is a positive number that is always subtracted from H_ps when evaluating NPSH_A.
• H_vp = The vapor pressure, in absolute units, of the liquid at the temperature it is being pumped. This term is subtracted in the equation because cavitation will happen if the absolute pressure inside the impeller eye or suction piping drops below the liquid vapor pressure. To account for that situation, we simply subtract the vapor pressure of the liquid being pumped. As with H_ps, this will require conversion from units of pressure to units of head.

Are you having air entrainment issues with your system? KSB tech services is equipped to help you with diagnostics and solutions. Reach out to KSB Service for all your pump service and repair needs.

Having defined terms, let’s apply it to a specific instance. Consider a pump mounted some distance away from an open-top tank. The liquid level inside the tank is 6ft (1.8m) above the centerline of the pump, which is at 4000ft (1219m) ASL. The liquid being pumped is water at a temperature of 120F (49C). Assume the total friction losses from the tank to the pump at the desired flow rate are 8ft (2.4m). The pump requires 17ft (5.2m) of NPSH_R at the desired flow rate. Will it cavitate?

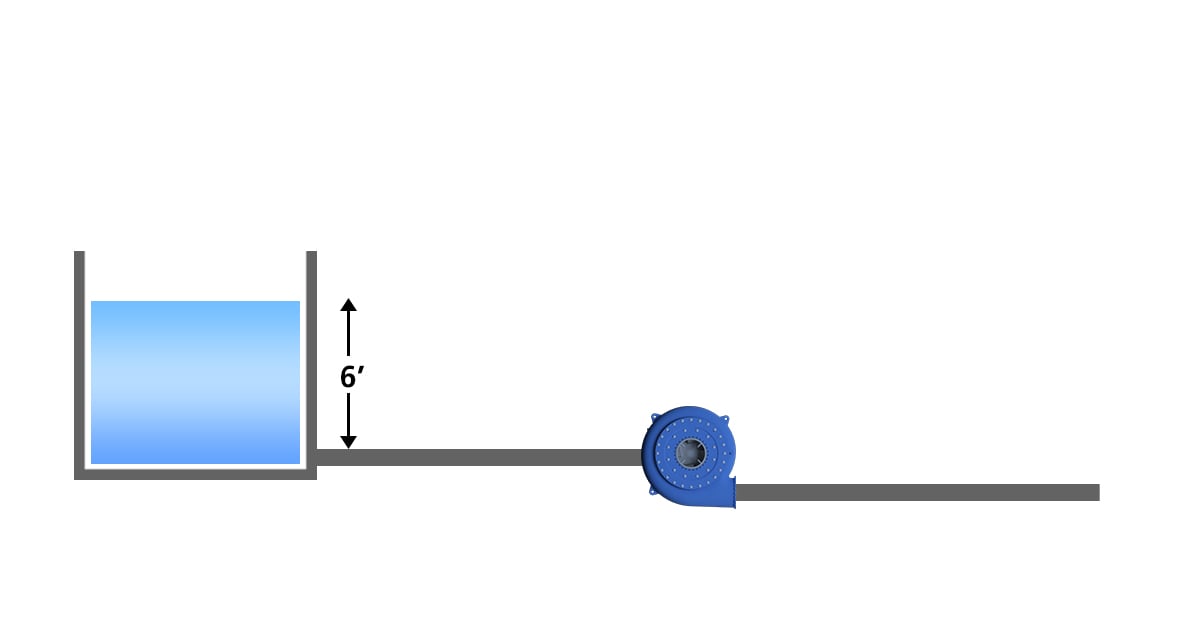
Diagram 1

Example situation:

• H_ps = 12.7psia (87.5kPa) since that is the average atmospheric pressure at 4000ft (1219m) elevation
• H_ss = 6ft (1.8m)
• H_f = 8ft (2.4m); Note that friction losses are not a constant, but rather a function of flow rate.
• H_vp = 1.7psia (11.6kPa); Vapor pressure of water at 120F/49C

NPSH_A is therefore:

12.7psia + 6ft – 8ft – 1.69psia (imperial units)

87.5kPa + 1.83m – 2.43m – 11.6kPa (metric units)

Well, not quite. The astute reader will note that it’s as difficult to add or subtract pressure and length as it is to add oranges to apples, so we must make sure that all terms have the same units before performing the calculation. NPSH calculations are made using “head,” and head is measured in units of length. It is known that a column of water exerts approximately 1psi of pressure for every 2.31ft of its height. In metric units a 1m column of water exerts 9.81kPa of pressure. So, 12.7psia (87.5kPa) of atmospheric pressure is equivalent to 29.3ft (8.9m) of head of water column. Similarly, 1.7psia (11.6kPa) of vapor pressure exerts a pressure equivalent to 3.9ft (1.2m) of water column. Substituting, we now have:

NPSH_A = 29.3ft + 6ft – 8ft – 3.9ft = 23.4ft (imperial)

NPSH_A = 8.9m + 1.8m – 2.4m – 1.2m = 7.1m (metric)

And since 23.4ft (7.1m) > 17ft (5.2m), NPSH_A > NPSH_R is satisfied, and the pump will not cavitate.

For the sake of simplicity, the example above was calculated using the vapor pressure of water at 120F (49C) and assumed a water specific gravity (SG) of 1.0. In actuality, water’s density varies with both temperature and pressure. For cases where the liquid SG is something other than 1.0, the SG of the liquid is required to make the conversion from pressure to head of liquid, in the following manner:

As above, assume local atmospheric pressure at 4000 ft (1219m) ASL is 12.7psia or 87.5kPa

This time, assume SG of the liquid being pumped is 1.1 (perhaps a light slurry of limestone)

Hps is then

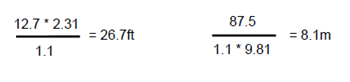Equation 2

H_vp should be converted in a similar manner so that it has units of head of the liquid being pumped.

Notice that NPSH is just an energy calculation, (e.g., Bernoulli’s equation). Since a centrifugal pump can’t add energy to a liquid until that liquid is inside the impeller, NPSH_A represents all the energy available to feed the pump. NPSH_R is essentially a measure of energy loss — measured as pressure drop — as the liquid enters the pump on its way to the impeller, where the pump can begin to add energy — in the form of pressure — back into the liquid. As long as NPSH_A > NPSH_R, cavitation will not pay an unwelcome visit to your pump installation.

Equation 3